Demystifying Namespace Merkle Tree (NMT): Exploring Soundness Analysis and Unveiling Partial Absence/Non-Inclusion Proofs

STB · 8 June 2023 23:31

Namespace Merkle Tree Soundness Analysis

Background

This document is motivated by a particular issue that identified the concept of a partial absence proof, raising questions about the validity and soundness of such proofs.

The underlying concern is that the usage of partial absence proof should not grant any undue advantage to an adversary in providing an absence proof for a namespace that actually exists in the tree.

To clarify, a partial absence proof deviates from the original NMT absence proof definition in a specific manner. Instead of returning the inclusion proof of the leafHash to the root (as proof.nodes), a partial absence proof returns the Merkle inclusion proof of one of the predecessors of the leaf (found along the branch connecting the leaf to the root). This predecessor’s namespace range does not overlap with the queried namespace (which is not present in the tree).

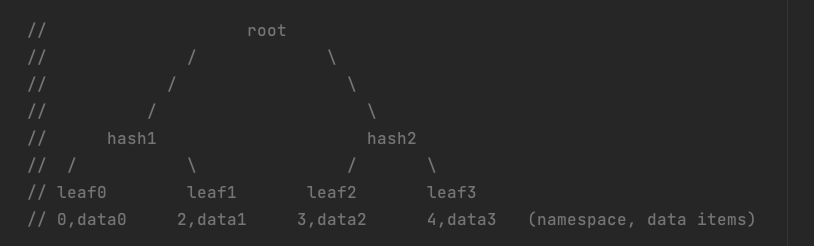
An illustration of a partial proof is given below:

A complete or normal absence proof for NID=1 would consist of: proof.start=1, proof.end=2, proof.leafHash=leaf1, and proof.nodes=[leaf0, hash2].
Partial proof, on the other hand, would have proof.start=0, proof.end=1, proof.leafHash=hash1, and proof.nodes=[hash2]. Note that the indices encoded in the partial absence proof don’t refer to leaf-level indices, but instead represent the index of certain intermediate nodes at a specific (higher) level, where nodes are zero-based indexed from left to right.

The remaining sections of this document aim to establish the soundness of partial absence proofs. To achieve this, we first introduce a formalized verifiable content-based query scheme, coupled with a detailed definition of desired security attributes, namely, inclusion soundness and absence soundness. This approach provides a foundation to comprehensively reason about the scheme and its characteristics, separate from the low-level construction details. Furthermore, it provides a framework for other similar schemes (if any) to compare with NMT.

Subsequently, we detail NMT as an embodiment of a verifiable content-based query scheme and provide its detailed construction. This section is analogous to the NMT specification, but it incorporates further formalization. Additionally, the original absence-proof generation and verification are substituted with the partial absence-proof variant.

Lastly, we provide formal proof that demonstrates NMT’s fulfillment of the soundness conditions for both inclusion and absence proofs.

Verifiable Content-Based Query (VCBQ)

From an abstract viewpoint, an NMT can be regarded as a data structure capable of performing verifiable content-based queries.
We declare that content NID matches data item d if they fulfill a specific relationship, Rel.
In simpler terms, Rel(d, NID) = true, where the relationship is defined by the respective scheme.
For the duration of this document, we use the term ‘match’ to signify Rel(d, NID) = true.
We describe a verifiable content-based range query scheme as one that incorporates the following polynomial-time algorithms:

param = Gen(security parameter) which creates the public parameters.
instance, digest = Init(param, U) takes a set of data items U and generates an instance together with digest as identifying information for the data set U.
Typically, the instance is used for proof generation whereas digest which is a more compact form of an instance is used for proof verification.
in_proof, D = InclusionProofGen(NID, instance) which generates a proof asserting that data items in D match the queried content NID, and are the only ones matching NID.
accept/reject = InclusionVerify(in_proof, D, NID, param, digest) verifies the correctness of the proof based on the system parameters and returns accept or reject accordingly.
abs_proof = AbsenceProofGen(NID, instance) which generates a proof asserting that there are no data items in D matching the queried content NID.
accept/reject = AbsenceVerify(abs_proof, NID, param, digest) verifies the correctness of the absence proof and returns accept or reject accordingly.

VCBQ Soundness

A VCBQ scheme should provide soundness for both inclusion proofs and absence proofs.

Soundness of Inclusion proof

For the inclusion proof, soundness can be broken down into the following properties:

Definition 1 (Inclusion): The inclusion property asserts that for every param = Gen(security parameter), instance, digest = Init(param, U), and in_proof such that InclusionVerify(in_proof, D, NID, param, digest) = accept, then it is guaranteed that all the data items in D belong to U. In other words, there does not exist any data item d' in D where d' does not belong to U or d' does not match the queried NID, except for a negligible probability.

Definition 2 (Completeness): The completeness property asserts that for every param = Gen(security parameter), instance, digest = Init(param, U), and in_proof such that InclusionVerify(in_proof, D, NID, param, digest) = accept, then D is whole, i.e., there does not exist any other data item d' not in U that matches NID, except for a negligible probability.

Definition 3: A VCBQ scheme (Gen, Init, InclusionProofGen, InclusionVerify, AbsenceProofGen, AbsenceVerify) provides soundness for inclusion proof if it satisfies inclusion and completeness as defined above.

Soundness of absence proof

Definition 4: A VCBQ scheme (Gen, Init, InclusionProofGen, InclusionVerify, AbsenceProofGen, AbsenceVerify) provides absence-proof soundness if for every param = Gen(security parameter), instance, digest = Init(param, U), and abs_proof such that AbsenceVerify(abs_proof, NID, param, digest) = accept, then there does not exist any item d in U that matches NID, except for a negligible probability.

NMT

NMT can be perceived as a verifiable content-based query scheme, conforming to the definitions outlined in the previous section.
Within the framework of NMT, a data item d is deemed to match NID - that is, Rel(d, NID) = true - if NID serves as a prefix to d.

param = Gen(security parameter): param consists of the Hash(.,.) function used for digest calculation and the namespace length NsLength which defines the length of NID.
instance, digest = Init(param, U) takes a set of data items U, whose first NsLength byte is treated as their namespace, which is the content by which the content-based queries are resolved.
This algorithm sorts U based on the namespace of its constituent items and constructs a namespace Merkle tree from U, using a modified hash function namely namespace hash function denoted by NsH(.,.) (for details please see the NMT specifications linked in the References section).
Init sets the instance to be that NMT structure.
Init outputs the NMT tree root R as the digest digest = R.
in_proof, D = InclusionProofGen(NID, instance) Takes instance and the namespace NID and outputs the namespace inclusion proof in_proof that consists of:
- A range start and end, indicating the range of the NMT leaves (data items in U) matching NID for which the proof is supplied.
- A set of nodes that constitute the Merkle index-based range inclusion proof of [proof.start, proof.end) to the tree root R.
accept/reject = InclusionVerify(in_proof, D, NID, param, digest) takes the in_proof and verifies its correctness as explained in the NMT specifications (there is a link to the specs in the References section).
abs_proof = AbsenceProofGen(NID, instance) which generates a proof asserting that there are no data items in the instance matching the queried NID. An absence proof abs_proof consists of:
- A subtreeHash (this differs from the original absence proof): to compute subtreeHash, we find the leaf in the tree with the smallest namespace larger than NID. Then we climb up the branch connecting that leaf to the root and find one of the parents/grandparents of that leaf whose namespace range has no overlap with the queried namespace (which is not present in the tree). The subtreeHash is the hash of that node.
- A range start and end representing the index of the subtree root subtreeHash in its respective level (where nodes at each level are indexed from left to right and are zero-indexed).
- A set of nodes that constitute the Merkle index-based inclusion proof of subtreeHash to the tree root R.
accept/reject = AbsenceVerify(abs_proof, NID, param, digest) verifies the correctness of the absence proof and returns accept or reject accordingly.
Essentially, it computes the NMT root using the Merkle inclusion proof provided in the abs_proof.nodes combined with the subtreeHash and verifies whether it matches the supplied root R.
Furthermore, it verifies that all nodes on the left side of the branch connecting subtreeHash to the root have a maximum namespace less than NID. Conversely, all nodes on the right side are expected to have a minimum namespace larger than NID.
The subtreeHash itself also needs to satisfy subtreeHash.minNs > NID.

NMT Soundness

NMT satisfies soundness for both inclusion proofs and absence proofs.

Inclusion Proof Soundness

We show that NMT satisfies both inclusion and completeness properties (as defined in Definitions 1 and 2), hence providing inclusion-proof soundness as defined in Definition 3.

Theorem 1: If the underlying hash function H(.,.) is collision-resistant then NMT satisfies the Inclusion property as defined in Definition 1.

Proof (by contradiction): Let in_proof' be an inclusion proof such that InclusionVerify(in_proof', D', NID, param, R) = accept.
Suppose there is an item d’_i in D' which does not belong to U.
Proof by contradiction: We show that if this happens, then the underlying hash function H is not collision-resistant, which contradicts the initial assumption.
We take the original set D where D and D' differ at least at their index i, and construct its inclusion proof in_proof.

Let Sib(d_i) and Sib(d'_i) be the sibling of d_i and d'_i.
These two nodes are either in D and D' or in the nodes of the in_proof and in_proof'.
Without loss of generality, assume Sib(d_i) and Sib(d'_i) are the right siblings.
Compute:

NsH(d_i, Sib(d_i)) = d_i.minNS || Sib(d_i).maxNS || H(d_i, Sib(d_i))
NsH(d'_i, Sib(d'_i)) = d'_i.minNS || Sib(d'_i).maxNS || H(d'_i, Sib(d'_i))

If NsH(d_i, Sib(d_i)) == NsH(d'_i, Sib(d'_i)), then we find a collision in the underlying hash function between d_i, Sib(d_i) and d'_i, Sib(d'_i).
If NsH(d_i, Sib(d_i)) ≠ NsH(d'_i, Sib(d'_i)), then we continue computing the other ancestors of d_i and d'_i up to the root until we hit two identical ancestors, namely N_l and N'_l, where l denotes the level of the node in the tree.
Let l be the lowest level at which the calculated parents have the same value (all the other parents in 0, ..., l-1 are different).
Such a node is guaranteed to exist, which is the root itself.

Let N_l = NsH(left, right) and N'_l = NsH(left', right') be such nodes, and left, right bring their children.
They differ at least in one of their right or left children (the one that resides on the branch connecting leaf i to the root).
This is the case due to the assumption we set out on l.
Without loss of generality, assume they differ at their right child, i.e., right ≠ right'.
Thus,

N_l = NsH(left, right) = (left.minNs || right.maxNs || H(left, right))
N'_l = NsH(left', right') = (left'.minNs || right'.maxNs || H(left', right'))

Since N_l = N'_l, we deduce H(left, right) = H(left', right'), and since right ≠ right', we have a collision in the hash function H.
This contradicts the initial assumption that the hash function is collision-resistant.
This concludes that the NMT inclusion proof satisfies the inclusion property.

TBD: We can also provide similar proof for the case that there cannot exist any item in D that does not match NID.

Theorem 2: If the underlying hash function H(.,.) is collision-resistant, then NMT satisfies the completeness property as defined in Definition 2.

Proof (by contradiction): Let in_proof' be an inclusion proof such that InclusionVerify(in_proof', D', NID, param, R) = accept.
However, suppose there exists a data item d'_k in U with a matching NID but not in D'.
In the NMT structure, it means that there exists a leaf d'_k with some index k which is not part of the in_proof’s range, i.e., k ∉ [in_proof'.start, in_proof'.end), as well as d'_k ∉ D', but its NID matches the queried NID.
k falls in the range covered by one of the nodes (subtree roots) in the proof.
Without loss of generality, suppose k < in_proof'.start (a similar argument applies to the case that k > in_proof'.end).
Suppose S is the node (the subtree root) in the in_proof' that represents the range containing the index k.
We know that InclusionVerify(in_proof', D', NID, param, digest) = accept.
Since S' is also part of the proof, hence S' is also authenticated (there is a valid set of hashes that combined with S' can result in R).
S' resides on the left side of the proof (this is because it covers k which is k < in_proof'.start), and hence is a left sibling.
Therefore, due to the completeness check done as part of the InclusionVerify, we know S'.maxNs < NID.
However, k (i.e., d'_k) falls in the index range of S'.
This indicates that S'.maxNs should be NID and not strictly less than NID.
This means that S''s namespace range differs from the same node in the original tree, i.e., S.
That is, S'.maxNs ≠ S.maxNs, thus S ≠ S'.
We compute the parent of S and S'. Let Sib(S) and Sib(S') denote the nodes in the in_proof and in_proof' (or computed using the proofs) that are siblings of S and S' respectively.

NsH(S, Sib(S)) = S.minNS || Sib(S).maxNS || H(S, Sib(S))
NsH(S', Sib(S')) = S'.minNS || Sib(S').maxNS || H(S', Sib(S'))

If NsH(S, Sib(S)) == NsH(S', Sib(S')), then we find a collision in the underlying hash function between S, Sib(S) and S', Sib(S').
If NsH(S, Sib(S)) ≠ NsH(S', Sib(S')), then we continue computing the other ancestors of S and S' up to the root until we hit two identical ancestors, namely N_l and N'_l, where l denotes the level at which this occurs.
Such a node is guaranteed to exist, which is the root itself.
Since l is the lowest level at which this difference exists, their children are not identical.

Let N_l = NsH(left, right) and N'_l = NsH(left', right') be such nodes, and left, and right being their children.
They differ at least in one of their right or left children (the one that resides on the branch connecting leaf S to the root).
Without loss of generality, assume they differ at their right child, i.e., right ≠ right'.
Thus,

N_l = NsH(left, right) = (left.minNs || right.maxNs || H(left, right))
N'_l = NsH(left', right') = (left'.minNs || right'.maxNs || H(left', right'))

Since N_l = N'_l, we deduce H(left, right) = H(left', right'), and since right ≠ right', we have a collision in the hash function H.
This contradicts the initial assumption that the hash function is collision-resistant.
This concludes that the NMT inclusion proof satisfies the completeness property.

Absence Proof Soundness

Theorem 3: If the underlying hash function H(.,.) is collision-resistant, then NMT satisfies the absence-proof soundness property as defined in Definition 4.

Proof: Let abs_proof' be an absence proof such that AbsenceVerify(abs_proof', NID, param, digest) = accept, however, there exists an item d' in U that matches NID.
In terms of NMT, it means there exists a leaf with some index k with namespace NID.
By construction, k falls in the range covered by one of the nodes in the proof.

Nodes of the proof are sorted based on the range of leaf indices they cover (based on the construction of the NMT proof).
N'_{k_1}, N'_{k_2}, ..., N'_{k*}, ..., N'_{k_n} where [k_1.start, k_1.end] ∪ [k_2.start, k_2.end] ∪ [k*.start, k*.end] ∪ [k_n.start, k_n.end] = [0, n] and all the ranges are non-overlapping.
They basically partition the index space of the tree leaves.
N'_{k*} is the one returned as the leafHash whose N'_{k*}.minNs > NID (part of the definition).
All the other nodes N'_{k_1}, N'_{k_2}, ..., N'_{k_n} are the siblings along the branch connecting N'_{k*} to the root.
According to the AbsenceVerify algorithm, the nodes on the left of N'_{k*} have the maximum namespace strictly less than NID, and all the nodes on the right side have the minimum namespace strictly greater than NID.
Without loss of generality, suppose S' to be the node in the set of nodes in the abs_proof', i.e., N'_{k_1}, N'_{k_2}, ..., N'_{k*}, ..., N'_{k_n}, that covers index k.

We also know that all these nodes are authenticated since AbsenceVerify(abs_proof = {nodes: {N'_{k_1}, N'_{k_2}, ..., N'_{k_n}}, leafHash: N'_{k*}, start: k*.start, end: k*.end}, NID, param, R) = accept, meaning that the abs_proof.nodes together with N'_{k*} correctly result in tree root R.
So S' is also authenticated.
Assume S' is on the left side of the range represented by N'_{k*} and hence is a left sibling (we can apply a similar argument by assuming S' is on the right side).
Therefore, S'.maxNs < NID (due to the completeness check done during AbsenceVerify).
However, k falls in the index range of S'.
This indicates that S'.maxNs should be NID and not strictly less than NID.
This means that S''s namespace range differs from the same node in the original tree, i.e., S.
That is, S'.maxNs ≠ S.maxNs, thus S ≠ S'.

Let proof be the Merkle inclusion proof of S to the tree root R.
We compute the parent of S and S'.
Let Sib(S) and Sib(S') denote the siblings of S and S' respectively (Sib(S') can be computed

using the nodes in the absence proof abs_proof', i.e., N'_{k_1}, N'_{k_2}, ..., N'_{k*}, ..., N'_{k_n}).

NsH(S, Sib(S)) = S.minNS || Sib(S).maxNS || H(S, Sib(S))
NsH(S', Sib(S')) = S'.minNS || Sib(S').maxNS || H(S', Sib(S'))

If NsH(S, Sib(S)) == NsH(S', Sib(S')), then we find a collision in the underlying hash function between S, Sib(S) and S', Sib(S').
If NsH(S, Sib(S)) ≠ NsH(S', Sib(S')), then we continue computing the other ancestors of S and S' up to the root, until we hit two identical ancestors, namely N_l and N'_l, where l denotes the level at which this occurs.
Such a node is guaranteed to exist, which is the root itself.
Since l is the lowest level at which this difference exists, the children of N_l and N'_l are not identical.

Let N_l = NsH(left, right) and N'_l = NsH(left', right') be such nodes, and left, right being their children.
They differ at least in one of their right or left children (the one that resides on the branch connecting leaf S to the root).
Without loss of generality, assume they differ at their right child, i.e., right ≠ right'.
Thus,

N_l = NsH(left, right) = (left.minNs || right.maxNs || H(left, right))
N'_l = NsH(left', right') = (left'.minNs || right'.maxNs || H(left', right'))

Since N_l = N'_l, we deduce H(left, right) = H(left', right'), and since right ≠ right', we have a collision in the hash function H.
This contradicts the initial assumption that the hash function is collision-resistant.
This concludes that the NMT absence proof satisfies the soundness property.

References

NMT specifications