Faster commitment construction over the square

[nashqueue]

Motivation

Each row and column is committed to in the erasure-coded data square. However, this commitment calculation can become a bottleneck for consensus for bigger squares, so we want to minimize the time it takes to calculate the commitment.

We can achieve the same properties an NMT tries to achieve while modifying the data structure.

Current Construction

Today, each row and column is committed to a namespaced Merkle tree, where each row and column has its own NMT.

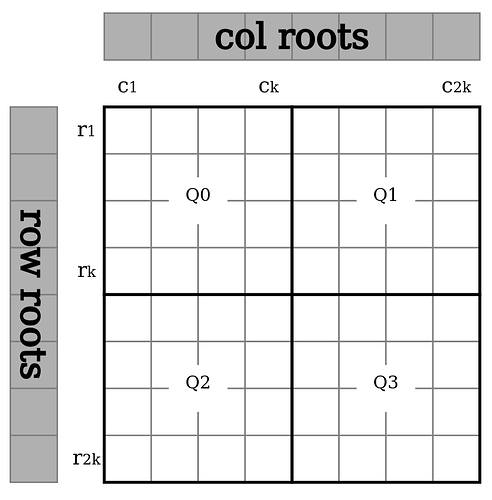
Diagram: Datasquare split into 4 quadrants where Q0 is the original data and the other quadrants erasure codes of that quadrant.

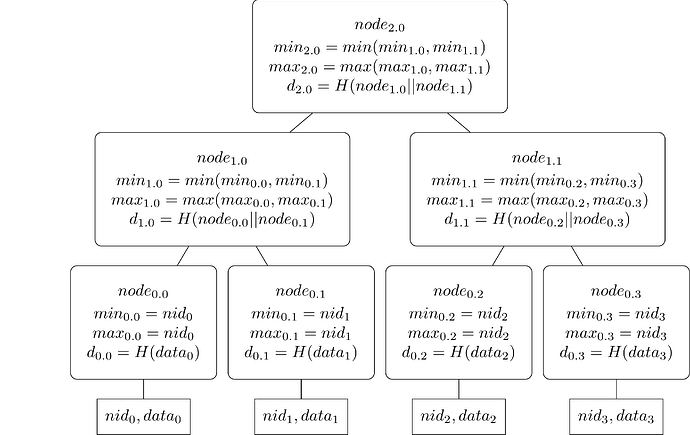
The NMT is inherently a complex data structure. A namespaced Merkle tree is an ordered Merkle tree that uses a modified hash function so that each node in the tree includes the range of namespaces of the messages in all of the descendants of each node. The leaves in the tree are ordered by the namespace identifiers of the messages. In a namespaced Merkle tree, each non-leaf node in the tree contains the lowest and highest namespace identifiers found in all the leaf nodes that are descendants of the non-leaf node, in addition to the hash of the concatenation of the children of the node. Source

The NMT results in bigger inner nodes as the namespace size is 29 bytes, so each node is 90 bytes in total. The bigger nodes then increase the number of hash cycles needed to create the commitment, which can be an execution bottleneck and increases the inclusion proof size for blobs and samples.

The goal of the NMT is to provide Merkle inclusion proofs to be created that prove to a verifier that all the tree elements for a specific namespace have been included in a Merkle inclusion proof. That guarantees that the rollup downloaded all the data without downloading the data from other rollup namespaces.

Optimization 1: The parity shares all have the same namespace. They don’t need an NMT.

Today, the parity shares are prepended by a reserved namespace 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF.

This means all parity shares have the same namespace. In practice, no rollup currently wants or will ever download all parity shares exclusively. Additionally, by pure positioning from the data root, you can imply the namespace, so we do not need this redundant information in each inner node of the tree.

Therefore, the parity shares should be a simple binary Merkle tree and do not have to be namespaced Merkle trees in the first place. We currently wrap parity shares in a namespace before committing them in a leaf for the NMT, but this part can also be removed. In general it would be best to remove the concept of namespaces in the parity shares as a whole.

For rows in Q2/Q3 and columns in Q1/Q3, the tree over the shares can be just a binary Merkle tree up to the row/column root, as all leaves are parity shares.

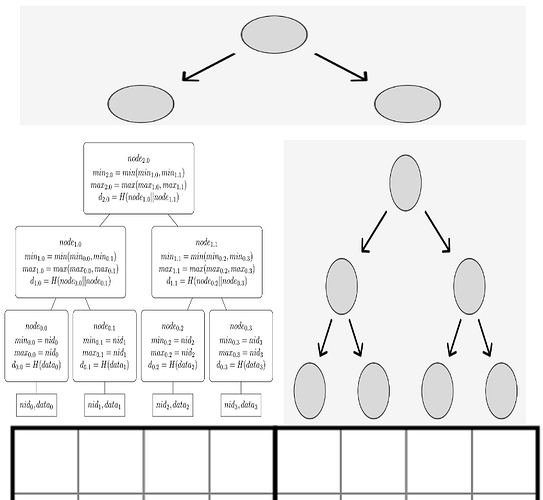
For rows in Q0/Q1 and columns in Q0/Q2 we need a more advanced tree structure, as part of the tree is an NMT. The picture below should illustrate how the first row of the square will be committed over.
The left side over the row above Q0 will be an NMT, and the right side will be a binary Merkle tree. The roots of both trees will be children of yet another short binary Merkle tree.

Optimization 2: Column roots don`t need the NMT

Going back to the goal of the NMT, it is to provide Merkle inclusion proofs to be created that prove to a verifier that all the tree elements for a specific namespace have been included in a Merkle inclusion proof.

There is no scenario in which rollups want that information over the column roots. Therefore, the commitment can be just a binary Merkle tree over the shares, disregarding the namespace information entirely. Rollups only request this information over rows, so providing this information in columns is a waste.

Unlocking 2 nice side effects

The first nice side effect is that the row and column roots are now only 32-byte large hashes instead of 90 bytes, as no root is an NMT root anymore. This reduces the size of the DAH by ~3x, which will help lower the light node requirements massively.

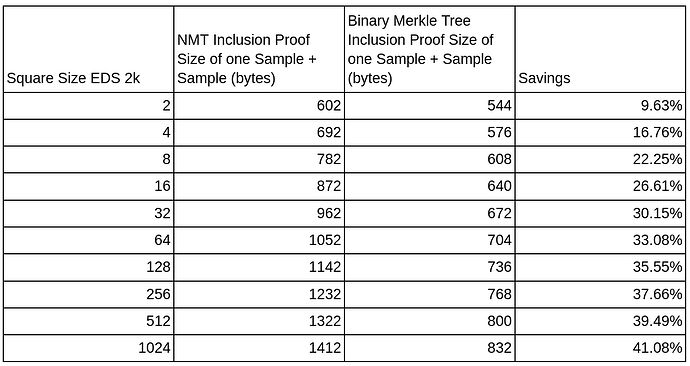
The second bonus is that we can now provide the samples by columns only. Currently, we are only sampling through rows, but nothing stops us from doing columns. This way, we can use the fact of the second optimization and guarantee a smaller proof size when sampling. This small table shows the improvements over different square sizes where the proof size is measured in bytes.

Conclusion

Both optimizations combined make it so we only need an NMT over the rows and only in Q0. This will reduce the computation overhead the NMT introduced. the We also reduce the size of the DAH by 3x and the proof size for samples if we sample over column roots.

The next thing to tackle is removing the namespace information from the shares and optimizing how we commit over the rows in Q0 more efficiently and user-friendly.

Thanks @adlerjohn for review

[nick]

Such seemingly simple changes with massive benefits! Nice work.

@nashqueue

This will reduce the computation overhead the NMT introduced

Do we have any sense of how much this would reduce computation overhead?

[nashqueue]

@nick

Do we have any sense of how much this would reduce computation overhead?

TL:DR From the get-go, we will reduce pure computation by 33%, with a potential of up to 67% with some additional tricks. My guess is that the most considerable speedup we will get is from reduced allocations and more efficient memory access. I don’t have any numbers on that.

Explanation:

One inner node in the NMT is 90 bytes. 29 + 29 + 32.

If you are hashing the children, then this results into

domain seperator + left_min_namespace + left_max_namespace + left_hash + right_min_namespace + right_max_namespace + right_hash = 1 + 90 + 90 = 181 bytes

181 bytes will turn, with the sha-256 algorithm, into two full blocks of data and one block for the remaining data + padding data, as one block can contain 64 bytes. Three blocks mean 192 rounds of hashing.

With 32 bytes, we will end up with 65 bytes of data (1 + 32 + 32), resulting in 2 blocks, meaning 128 rounds of hashing. (33% faster)

Interestingly, we chose a 29-byte namespace instead of a 32 one to decrease the number of blocks from 4 to 3.

With 2 additional tricks laid out by Preston here, we can reduce it to 1 block. In particular, we can use one bit instead of one byte for the domain operator and take it from one of the hash digests. Finally, we can halve the compressions by removing the padding for sha-256 as our internal nodes have fixed lengths. (Note don’t try this at home due to length extension attacks; always under the supervision of a qualified cryptographer)