Motivation
The data availability header (DAH) consists of row and column roots. These are the roots of the namespace merkle tree (NMT) that spans over each row and column over the extended data square (EDS).
This DAH must be downloaded and stored in each light node. If one row root is 90 bytes large (min namespace (29 bytes) + max namespace (29 bytes) + 32 bytes hash), then the biggest block of 8 MB (256*256 shares) would produce a DAH of 46 KB (90*2*256).
Storing this for 3 weeks and downloading it each block is nothing compared to a full node, but that does not make it possible to run a light node on a toaster. So we can ask ourselves if we could stop downloading the DAH without consequences, and the answer is unfortunately no.
We have two competing objective functions at play. One wants to minimize the size of a bad encoding fraud proof, and the other wants to minimize the amount that we have to download; the less you download, the bigger the expected fraud proof will be. We will show this with a counterexample.
Consequences
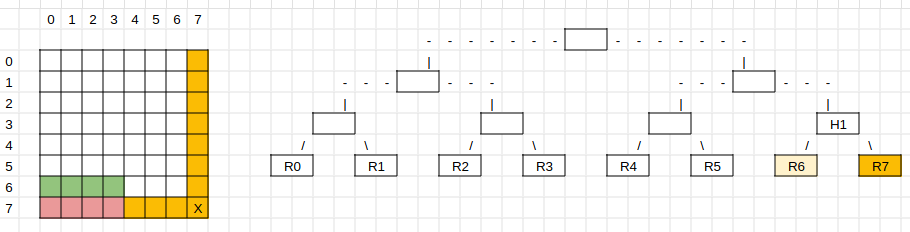
Let’s say we don’t have the data availability header. This means that we don’t have the row and column roots of the square by default. While sampling the square, we also sample the row and column roots. The square has rows and columns from 0 to 2k-1, where 2k is the size of the square (EDS).
Now, let’s assume the row and column roots 2k-c are hidden, depicted in yellow for c=1. Hidden means that you cannot sample them. This is possible because, with a square large enough, most light clients will be fooled into thinking that the square is available even though a row and a column are hidden. These kinds of withholding attacks are allowed to hide, at most, a constant number c of rows and columns.
The share with X is badly encoded. That means that the full node has to give a fraud proof to the light node that the share is badly encoded. The full node also cannot access the row root R7 in this example, as the DAH is missing, and that row cannot be sampled, which means that a full node cannot get that information from a light node. We will only look at row roots as the example, which is equivalent to columns in this construction.
How can the full node prove that the share in the row is badly encoded? It proves this by providing share inclusion proofs of the shares of row 2k-1 through the col roots 0 to k-1 (red shares). Usually, the light node would get those shares, encode them, and, with the full row, have the preimage of the row root 2k-1 and check against it.
Let’s assume we have the row root 2k-2 or, in this case, R6. Given R6 and half of the shares below R7, we can calculate the parent H1 and check against this commitment, which we assume we already know.
Now, let’s assume R6 is also hidden. In this case, we will need an additional half of the shares below R6 (green shares) to calculate the preimage of the parent H1. The conclusion is that with each level of hidden rows, the bad encoding fraud proof size doubles. This breaks the requirement of having compact fraud proofs if there is no DAH. Light nodes will be more and more likely to detect hidden rows, but not likely enough for light nodes to have high confidence in availability.
You could argue that we can reduce the height of the DAH by a constant amount if we are ok with increasing the fraud proof size by the same constant amount.
Conclusion & Alternative
The data availability header has to be available (no more or less, which is a clue for a future idea).
The original motivation was to see how we can minimize the amount of data a light node has to download without compromises. We saw that we could make the DAH smaller, with the consequence of increasing its fraud-proof size. I want to end the post with a quick optimization that will reduce the amount of data to be downloaded by 3x.
We can do that by using the hash of the NMT root (32 bytes) instead of the full NMT root (min nid | max nid | hash). The merkle tree over all row and column roots is a standard binary tree and not an NMT because it is impossible to construct an NMT with the current structure. The NMT roots are the preimages of the leaves of this binary tree, and I suggest using the leaves instead of the NMT roots.
The availability guarantee and the fraud proof size do not change. The only downside is that the light node has to compute 1 extra hash operation for each proof that it verifies. Still, it can reduce the overall bandwidth requirement for the DAH by 3x, which could end up taking the most bandwidth in the future when blocks are constantly the maximum size. We should also not that the DAH size will double with each block size increase.