A critical component of Celestia’s security is the Data Availability Sampling (DAS) process. As part of this process, nodes in a peer-to-peer network request random samples from other nodes.
The selective disclosure attack
One attack vector is selective share disclosure (§ 5.4), whereby an adversary A tries to trick an honest node into accepting an unavailable block. Briefly:
- A wants to withhold enough shares, s.t. the block is unrecoverable;
- A wants to respond to all queries by a client C, s.t. C is convinced that the block is available.
Model
The model is the following:
- Peer-to-peer network. Additional privacy solutions, e.g. Tor, can be layered on top.
- Requests are pushed/initiated by honest nodes.
- The adversary can run a limited number of nodes; DDoS attacks are not in scope.
- Adversarial nodes are indistinguishable from honest nodes, so they cannot be blacklisted as long as they never respond incorrectly. (Adversary nodes may be blacklisted if they attempt to DoS an honest node and are identifiable.)
A suggested solution to selective share disclosure is an anonymization layer. This prevents the adversary from being able to link requests to their origin.
Analysis
We assume an ideal private network: “different sample requests cannot be linked to the same client, and the order that they are received by the network is uniformly random with respect to other requests” (cf. § 5.4).
Following, we conduct simulations to estimate the probability of a selective disclosure attack succeeding under this setting. Each block is organized in a matrix of k*k shares, before the RS code is applied on it; in our simulations, we set k=128.
Briefly, each block comprises 4k2 shares that form the 2D Reed-Solomon matrix. To reconstruct the block, the parties need to collectively get up to ¾ of the shares, so the adversary needs to deny queries for at least ¼ of those shares. We assume that the shares that need to be denied are chosen by the adversary a priori, i.e., at the moment of the block’s creation. Each client samples s shares and queries the attacker for them. If the attacker replies to all queries, i.e., if no query relates to one of the k2 shares that the attacker would deny, then the attack is successful. The number of all clients is c.
The first simulation runs 106 independent tests. Therefore, it measures the probability of an attack being successful to a degree of 6 decimal points. Equivalently, it measures the expectation of an attack occurring every 106 blocks.
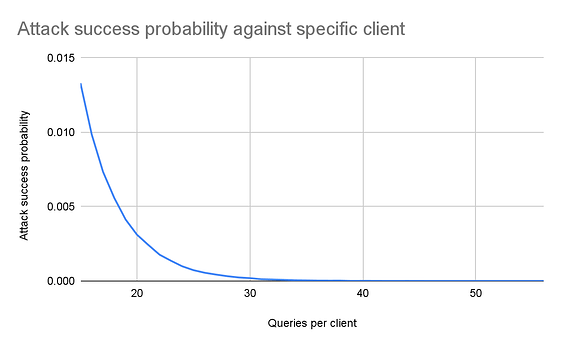
Figure 1 shows the probability that an attack is successful against a specific client. In this scenario, the adversary wants to convince a specific client that a block is available (while, in reality, it is not). Since each client chooses their shares (to query) independently and since the adversary cannot attribute each query to its source client, the probability depends only on s (the number of queries that the client makes). As can be seen, if the client makes 15 queries, the possibility that none of them corresponds to a withheld share is 0.0133. Equivalently, if the attacker continuously tries to trick the client, the attack will succeed on expectation after 75 tries. However, if the client makes 50 queries, the simulation returns 0, i.e., the probability drops to below 10-6.
Figure 1. The successful attack probability against a specific client.
The second scenario is an attack against any client. This simulation runs 103 independent tests. Here, instead of targeting a specific client, the adversary wants to convince some client that the block is available. Again, the probability that each client is successfully attacked depends on the number s of queries. However, since each client operates independently, the probability of this attack succeeding increases with the number c of clients (as long as s < k2). For example, if 50 clients make 15 queries each, the probability of a failure for some block (i.e., one of the clients accepting a specific unavailable block) is 0.46; in contrast, under 400 clients the probability increases to - effectively - 1. Interestingly, the probability drops significantly as the number of queries increases. For example, setting s=40 reduces the attack’s probability to less than 0.01 for all numbers c that were tested. (A figure of the relevant simulation is available here).
Discussion
First, the above simulations show that using a private network (even an ideal one) does not necessarily protect against the selective disclosure attack. Instead, the number s of queries that each client makes should be carefully chosen to reflect the success probability of the attack (equiv. the confidence of each client when marking a block as available).
Second, in the research paper (and the above simulations), it is assumed that the shares are set as unavailable a priori. However, an adversary could choose which shares are unavailable adaptively, i.e. after having replied to some queries. Specifically, the adversary can reply to queries as long as the set of queried elements is not sufficient to construct the matrix .
On average, accounting for repetitions in the sampling, we require slightly over 6000 clients to guarantee that ¾ of the table has indeed been queried. However, using RS error correction, clients can also derive unqueried elements as long as enough of their neighbors have been queried. For k=128, s=15 ca. 2600 clients should be enough. This is lower than the values from Table 1: the analysis in the paper assumes that for recovery, querying ¾ of the shares is necessary (rather than sufficient).
Third, a private network with the necessary requirements described above does not currently exist at production level. Some theoretical works do offer proof of concept implementations:
- Atom: Horizontally Scaling Strong Anonymity
- Stadium: A Distributed Metadata-Private Messaging System
These protocols guarantee the theoretical “enhanced” network that is assumed in the research paper, i.e., uniform message delivery and sender anonymity. However, there exists no production-ready implementation, through which Celestia messages can be directly routed. In addition, their contributions are somewhat too theoretical, in the sense that they can’t scale to large numbers of nodes.
There exist some up-and-running networks that offer metadata (i.e., source) anonymity:
- Tor
- NYM
However, these networks don’t present uniform delivery of messages. Therefore, an adversary could cluster queries based on timing assumptions. Specifically, assume that: i) an honest node issues its queries altogether, instead of introducing artificial delays (which would increase latency); ii) the clients don’t all make their queries at the same time, but with some delay between them (e.g., in the order of a few hundred milliseconds, which is the latency of Tor). A receiver would observe the queries arriving in batches and could then cluster them, s.t. with high probability all queries in a cluster correspond to the same client. Consequently, the attacker could more easily mount a targeted attack against particular clients (cf. § 5.7, Standard Model).
In conclusion, our analysis shows that assuming an ideal, private underlying network is both not realistic, as no such production-ready system exists, and insufficient, depending on the other parameters of the system. As a result, enhancements in other aspects of the system are needed to protect against selective disclosure attacks.