ZK-Proving DAS [PART 1]: Intro

[garvitgoel]

Brought to you by Electron Labs

#zkDAS

A simple concept note to discuss how we can zk-prove DAS.

Motivation -

Celestia has very light node, but it can be made Ultra light, by orders of magnitude.

However, this requires zk-proving DAS, which is not well understood. Hence I am writing this article.

How can we ZK-prove data availability?

Background

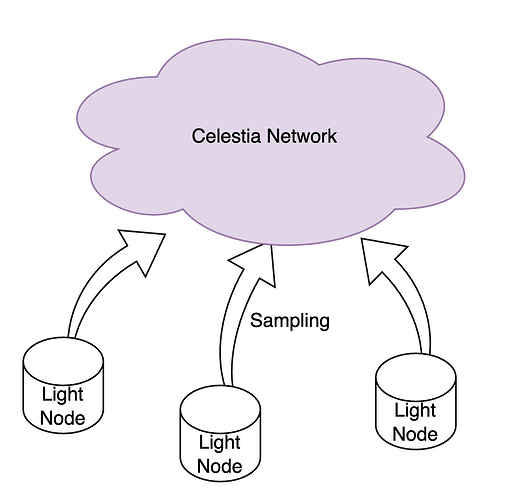
The goal behind data availability sampling in the Celestia network is to provide guarantee that the data is available with the network.

Celestia currently achieves this by having a large number of light clients participate in the network. The assumption is that if many light clients continuously sample the network for bits of data, together these light clients will sample enough data from the network resulting in very high probability that the data is available. Details of how this works is better explained in Celestia docs.

Our Solution

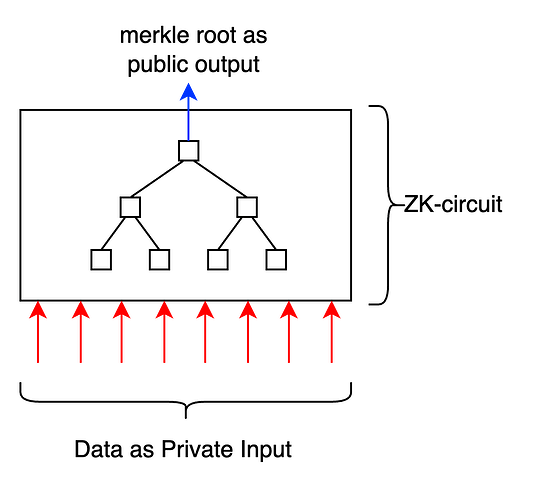
Let us now jump to solution where you can zk-prove DAS. Let us say that a certain entity (referred to as “DA prover” henceforth) in the Celestia network wants to prove that they have the data with them. Another entity (DA Verifier) will verify this claim and we assume that they have limited bandwidth and computational resources (say mobile phone or chrome extension). We assume that the merkle root of the said data is already publicly known.

To prove data availability, the DA prover can simply use a zk-circuit that takes in the required data as private inputs and calculates it’s merkle root. The merkle root is given out as a public output.

This circuit (in plain English) proves that -

The DA prover has all the pieces of data which when merklized results in the given merkle root.

Since the data is given as private input to the circuit, it does not have to be shared with the verifier. The DA verifier only needs the zk-proof and the merkle root to verify this claim. Interestingly, the computational load on the DA verifier does not increase as the data in the network increases. This is because zk-proofs (groth16) can be verified in constant time.

Note: The DA prover will only be able to construct this proof successfully if they have ALL the data with them. It will be impossible to construct this proof even if just 1 bit of the data is missing.

Question: What is the guarantee that the DA prover has all the block data?

Answer: The fact that proof was generated and successfully verified provides a guarantee that the data was available with the DA prover.

However, since Celestia is supposed to handle very large amounts of data, it maybe difficult to construct this zk-proof since groth16 does not scale well with large amounts of data. We can use proof recursion methods to solve this issue, which is discussed in later sections.

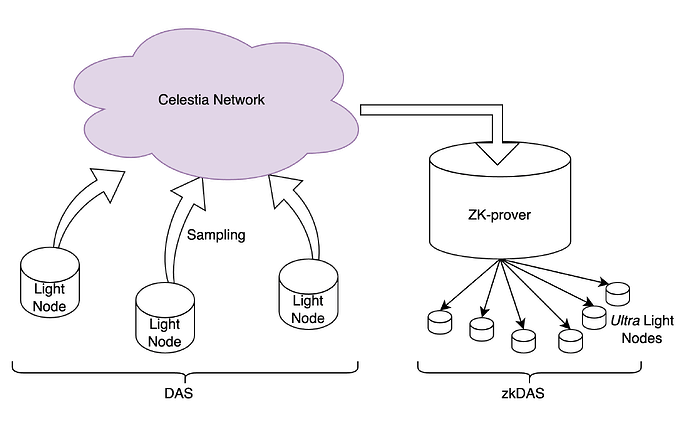
Benefits of zkDAS

Using zkDAS, we can construct a ZK based Ultra Light Client for the Celestia network. This will have many advantages -

1. This will enable Celestia chain can to run at a lower Blocktime. It is my understanding that Celestia plans to use 11.66 s as the blocktime, and the reason we are not going any lower is to keep the burden on the light clients low.
2. Have a large number of light clients in Celestia network is super important for the security of the network. Our approach will lighten the computational requirements from the Celestia light clients by orders of magnitude, enabling a much larger number of Celestia light nodes to exist, thereby improving security.
3. This will make it possible to run the Celestia light client as an Ethereum smart contract. Given that Ethereum itself will be able to verify DA, this will massively increase the security for DA for Ethereum rollups, and may even unlock new possibilities.
4. This model will not require any changes to Celestia core infrastructure. One can simply start running zk-provers for DAS.
5. In fact, the current light clients for Celestia can continue to operator as is, without being aware of the zk-provers, and continue to provide security to the network.

Incentivising creation and operation of zkDAS nodes.

We believe that zkDAS can become part of the Celestia node infrastructure itself. Similar to Celestia validators, DA prover operators can earn rewards and tokens for generating valid zk-proofs. Having said that, I think other ideas can and should be explored.

How will the ZK-prover technology work?

Using proof recursion to make the ZK-prover feasible

Celestia needs to deal with large volumes of data. This will require a large merkle tree being constructed inside the zk-circuit. It is infeasible to perform this operation inside a single groth16 circuit due to -

1. size of data that needs to be loaded to the circuit and
2. For a 6.4GB of data, the hashing operations for calculating the merkle root will require 3.2 trillion constraints (reference - https://ethresear.ch/t/benchmarking-zkp-development-frameworks-the-pantheon-of-zkp/14943), which is not feasible at all in groth16.

We believe this can be easily achieved using recursive proving schemes out there. We won’t compare different recursive systems with each other here, instead let us look at a circuit tree construction that can help us achieve this.

In the following section, we assume that the data is arranged as a large array and we shall discuss how we can calculate and prove the merkle root of the same. Let’s get started.

We start with a large array containing N items {item_{0}, item_{1} … item_{n-1}}. We assume that the verifier only has the merkle root (root\_hash) of this array. We want to create a zk-proof that the merkle root of the array is root\_hash.

Let us start understanding this by starting with the leaf circuits.

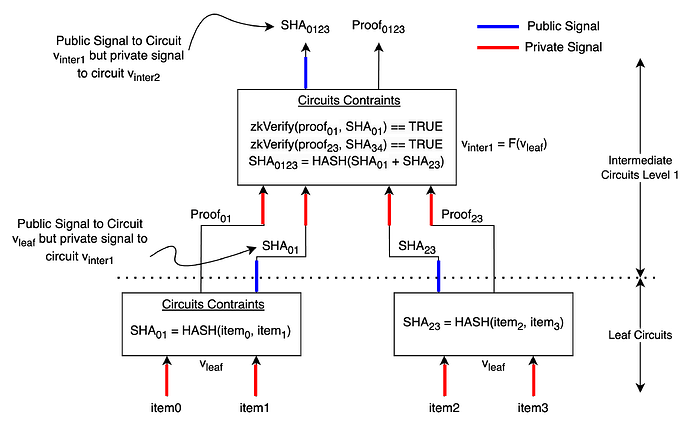
Leaf Circuit -

Private Signals: item_0 , \space item_1

Public Signals: SHA_{01}

Circuits Constraints:

1. HASH(item_0 , item_1) == SHA_{01}

Resultant Proof: SHA_{01}, Proof_{01}

This circuit proves that the prover is in possession of two inputs which when hashed together results in the value SHA_{01}.

Note: We must keep SHA_{01} as a public signal to ensure that Proof_{01} cannot be validated without SHA_{01}, thus establishing a link between the two. This is useful for upper intermediate circuits.

We can now take two such circuits and recursively combine them together into a single circuit as show in the intermediate circuits level 1 in the diagram above.

Intermediate Circuit Level 1 -

This is the circuit just above leaf circuits.

Private Signals: SHA_{01},\space Proof_{01}, \space SHA_{23},\space Proof_{23}

Public Signals: SHA_{0123}

Circuits Constraints:

1. zkVerify(proof_{01}, SHA_{01}) == TRUE
2. zkVerify(proof_{23}, SHA_{23}) == TRUE
3. HASH(SHA_{01} , SHA_{23}) == SHA_{0123}

Resultant Proof: SHA_{0123}, Proof_{0123}

This circuit proves that the prover has have all the elements of an array whose merkle root is SHA_{0123}

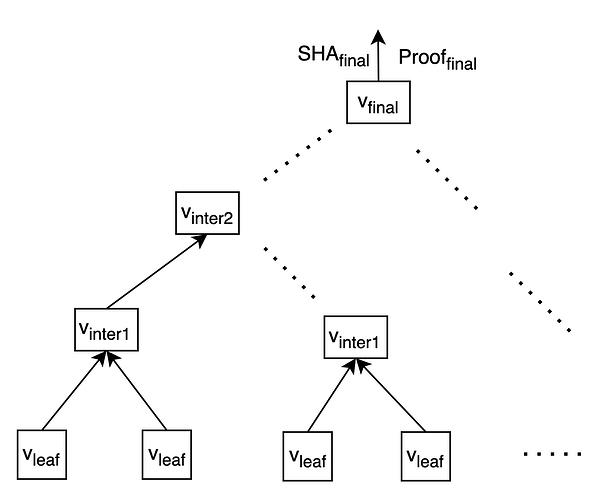
We can easily scale out this concept to a larger number of leaf nodes as shown below -

Finally, the verifier can check if SHA_{final} == root\_hash and that the Proof_{final} is valid.

The final proof Proof_{final} proves that the DA prover has have all the elements of an array whose merkle root is SHA_{final}

Next Steps

1. We invite the Celestia community to provide their thoughts about this. This is a very early concept note, and lot’s of community feedback will help us make it better, and find potential issues in the model. We would be happy to host a discussion within the Celestia community to dig deeper into this model.
2. If the Celestia community is excited about this, then we should build this!

[evan]

@garvitgoel

they have ALL the data with them. It will be impossible to construct this proof even if just 1 bit of the data is missing.

this a good write up @garvitgoel, thanks for this

for data availability sampling, the light client is not just trying to prove that the server has all of the data, but that anyone can download the data (that the data was published). In the above scenario, would it still be possible that the server compute a proof, but hides data?

[garvitgoel]

Thank you so much for this @evan . I took sometime to reply since I wanted to spend some time thinking about your question.

I have taken the following assumption in my reply. Please let me know if it is wrong -

The light node network collectively samples only the latest block. Once a light node is satisfied with the sampling it has done for a given block, it moves to the latest block it has recieved. I believe the duration for which a light node samples a given block is the Celestia blocktime (~11.6s)

Now, to answer your question -

You said that the data is downloadable in the current Celestia model. However, light nodes only sample a given block for a short while, hence even if the light clients prove that the data is downloadable, this gaurantee is only valid for 11.6 s. It is entirely possible that the block producer start withholding the data later on.
However, in Celestia’s current model, the existence of full nodes provide the gaurantee that “at least somone will share the data” in case the block producer refuses to share the data.

In our proposed zk based model, since there is no sampling happening, full nodes don’t really receive the samples from light clients, and hence they have no way of generating the full block.
This might introduce another problem ⇒ how do you generate fraud proofs of invalid blocks. This might be fixable by generating zk-proofs of correctness of erasure coding itself, but I think that might be a discussion for another day.

Having said all this, I think our proposed scheme would introduce two problems -

1. How do you ensure that atleast one node has the data available with them? (since full nodes are not possible in our model)
2. How do you generate fraud proofs of invalid erasure coding?

We will try to solve these issues and come back with a better solution.

[nick]

Unfortunately I think that the only way the DAS scheme can work is if the light node actually downloads the samples directly. I don’t think you can get around this requirement by using a zk scheme.

However, there are ways in which we can use zk to improve the DAS scheme. A big one is what you mention above:

generating zk-proofs of correctness of erasure coding itself

If you created a way to generate a zk proof of correct erasure coding, then light nodes would not have to wait for a fraud proof window after sampling each block to consider it final. Second, we wouldn’t need bad encoding fraud proofs (BEFPs) which require the light node to download an entire row or column of the block data. Third, this unlocks the possibility of having consensus nodes vote on blocks without downloading all the data.

I think this would be a valuable thing to try and build. I talked about this and other zk based improvements to Celestia in my talk at research day: https://www.youtube.com/watch?v=NCLuU-NS3IU

[garvitgoel]

Thank you so much for pointing this out @nick We were also leaning towards zk-proving erasure coding itself.

In the video, you mentioned that ZK-tech itself is not ready for proving erasure codes. I agree that simple groth16 will not work here. I strongly believe recursion is the way to go.

We are not too far from deploying a recursion based ZK Light Client on testnet. You can expect to hear more from us in near future

[colludingnode]

Validity-proving erasure coding is interesting, because an erasure coding validity proof is fundamentally the same as a polynomial commitment / low-degree test!

A good place to start is here

[drmpl]

@nick

Second, we wouldn’t need bad encoding fraud proofs (BEFPs) which require the light node to download an entire row or column of the block data.

So if we could generate correct erasure coding proofs, we would be able to use the Strawman 1D Reed-Solomon?